Tutorial Sage
Álgebra Linear
| Operação Matemática | Sintaxe Sage | Exemplo | Resultado |
| Sistema Linear $ Av=b$ | A.solve_right(b) | A=matrix([ [1, 2, 6], [ 1, 2, 0 ], [ 1, -2, 3 ] ] ) b=vector( [1, -1, 1] ) A.solve_right(b) |
( -1/2, -1/4, 1/3 ) |
| Núcleo de A |
kernel( A ) |
A=matrix( [ [1, 2, 3 ], [ 1, 2, 3], [ 1, 2, 3] ] )
|
( 1, 0, -1 ) ( 0, 1, -1 ) |
| Polinômio caracteristico de A | A.charpoly() |
A=matrix( [ [1, 2, 3], [ 1, 2, 3 ], [ 1, 2, 3 ] ] )
|
x^3 - 6*x^2 |
| Autovalores de A | A.eigenvalues() |
A=matrix( [ [1, 2, 3 ], [1, 2, 3 ], [ 1, 2, 3] ] )
|
[ 6, 0, 0 ] |
| Autovetores de A | A.eigenvectors_right() |
A=matrix( [ [ 1, 2, 3 ], [ 1, 2, 3], [ 1, 2, 3] ] )
|
[(6, [ (1, 1, 1) ], 1), (0, [ (1, 0, -1/3), (0, 1, -2/3) ], 2)] |
Mais sobre o tópico: ![]() quickref-linalg.pdf
quickref-linalg.pdf
Referência: Documentação Sage
Derivada
| Operação Matemática | Sintaxe Sage | Exemplo | Resultado |
|
$\displaystyle\frac{df}{dx}$ |
diff( f , x ) |
diff( sqrt(x), x) |
|
|
$\displaystyle\frac{d^nf}{dx^n}$ |
diff( f, x, n ) |
diff( sin(x), x, 3) |
-cos(x) |
|
$\displaystyle \frac{\partial f}{\partial x}$ |
diff( f , x ) |
var( 'y' ) |
2*x |
|
$\displaystyle\frac{\partial^2f}{\partial y\partial y}$ |
diff( f, y , y ) |
var( 'y' ) |
2 |
|
$\displaystyle\frac{\partial^2f}{\partial x\partial y}$ |
diff( f , x , y ) |
var( 'y' ) |
0 |
|
$\displaystyle\frac{\partial^2f}{\partial y\partial x}$ |
diff( f ,y , x) |
var( 'y,z' ) |
2*y |
Mais sobre o tópico: ![]() quickref-calc_1.pdf
quickref-calc_1.pdf
Referência: Documentação Sage
EDO
| Operação Matemática | Sintaxe Sage | Exemplo | Resultado |
|
EDO de 1ª Ordem $y'(x) + py(x) =q$ |
desolve( edo , y) | y = function( 'y' )( x ) show( desolve( diff( y, x ) + y - 1, y ) ) |
$\newcommand{\Bold}[1]{\mathbf{#1}}{\left(C + e^{x}\right)} e^{\left(-x\right)}$ |
|
EDO de 2ª Ordem $y''(x) + py'(x)+ ky(x)= q(x)$
|
desolve( edo , y ) | y = function( 'y' )( x ) show( desolve( diff( y, x, 2 ) - y == x , y ) ) |
$\newcommand{\Bold}[1]{\mathbf{#1}}K_{2} e^{\left(-x\right)} + K_{1} e^{x} - x$ |
|
Problema de Valor Inicial $y'(x) + py(x) =q$ $y( x_0 )=y_0$
|
desolve(edo , y , ics=[ x_0, y_0 ] ) | y=function( 'y' )(x) desolve( diff( y, x ) + y - 1, y, ics=[ 10, 2 ] ) |
$\newcommand{\Bold}[1]{\mathbf{#1}}{\left(e^{10} + e^{x}\right)} e^{\left(-x\right)}$ |
Mais sobre o tópico: ![]() solving_ordinary_differential_equations_-_sage_reference_manual_v7.pdf
solving_ordinary_differential_equations_-_sage_reference_manual_v7.pdf
Referência: Documentação Sage
Funções Matemáticas
|
Operação Matemática |
Sintaxe Sage |
Exemplo |
Resultado |
|
Valor Absoluto de $x$ |
abs( x ) |
abs( -2 ) |
2 |
|
Raiz quadrada $ x$ |
sqrt( x ) |
sqrt(225) |
15 |
|
Raíz de $x$ ordem $n$ |
x**( 1/n ) ou x^( 1/n ) |
8**( 1/ 3 ) |
2 |
|
Exponencial na Base $e$ |
exp( x ) |
exp( 2 ) |
e^2 |
|
Logaritmo Natural de $x$ |
ln( x ) |
ln( e ) |
1 |
|
Logaritmo de $x$ na Base $b$ |
log( x , b ) |
log( 1024,2 ) |
10 |
| Seno de x | sin( x ) | sin( pi ) | 1 |
| Cosseno de x | cos( x ) | cos( pi/2 ) | 0 |
| Tangente de x | tan( x ) | tan( 3*pi/4 ) | -1 |
| Secante de x | sec( x ) | sec( pi/3 ) | 2 |
| Cosecante de x | csc( x ) | csc( pi/3 ) |
2/3*sqrt(3) |
| Cotangente | cot ( x ) | cot( pi/3 ) | 1/3*sqrt(3) |
|
Coeficiente Binomial de $n$ sobre $r$ |
binomial( n, r ) |
binomial( 5, 2 ) |
10 |
|
Fatorial de $n$ |
factorial( n ) |
factorial( 5 ) |
120 |
|
Fatoração de primo de $n$ |
factor( n ) |
factor( 12 ) |
2^2*3 |
|
MDC de $a$ e $b$ |
gcd( a, b) |
gcd( 12, 16 ) |
4 |
|
Valor Máximo |
max( x,y,z w,... ) |
max( 1, 2.7, 4.8 ) |
4.8 |
|
Valor Mínimo |
min( x,y,z w,... ) |
min( 1, 2.7, 4.8 ) |
2.7 |
|
Menor Inteiro maior ou igual a $x$ |
ceil( x ) |
ceil( 1.4 ) |
2 |
|
Maior Inteiro menor ou igual a $x$ |
floor( x ) |
floor( pi ) |
3 |
|
Inteiro mais próximo ou igual a $x$ |
round( x ) |
round( 2.8456 ) |
3 |
|
Parte inteira $x$ |
int( x ) |
Int ( 2.8456 ) |
2 |
|
Número aleatório maior ou igual a zero e menor que 1 |
random() |
random() |
0.7311469958220904 |
|
Número inteiro aleatório em $[a,b]$ |
randint( a , b ) |
randint(1, 100 ) |
46 |
Mais sobre o tópico:
Referência: Documentação Sage
Gráficos
| Gráficos 2D | Sintaxe Sage | Exemplo | Resultado |
| Função $f$ | plot( f , ( x, a, b ) ) | plot( x^2, ( x, -1, 1) ) | 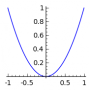 |
| Curva Paramétrica |
parametric_plot( [ x( t ) , y( t ) ], ( t, a, b ) ) |
var( 't' ) |
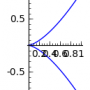 |
| Curva Implicita C | implicit_plot( C, (x, a, b), (y, c, d ) ) | var( 'y' ) implicit_plot( x^3+y^3 == 3*x*y, ( x, -3, 2 ), ( y, -3, 2 ) ) |
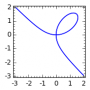 |
| Curva em coord. Polares | polar_plot( r(theta), ( theta, a, b ) ) | var( 'theta' ) polar_plot( theta/2*pi, ( theta, 0, 2*pi ) ) |
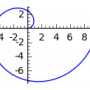 |
| Gráficos 3D | Sintaxe Sage | Exemplo | Resultado |
| Quádricas | plot3d( f, ( x, a, b ) , ( y, c, d ) ) | var('y') plot3d( x^2 - y^2, (x, -1, 1 ), ( y, -1, 1 ) ) |
 |
| Funções | plot3d( f, ( x, a, b ) , ( y, c, d ) ) | var('y') plot3d( e^(x/5)*sin(y), ( x,- 5, 5 ), ( y, -5 ,5 ) ) |
 |
| Superfícies Paramétricas | parametric_plot3d( [ x( u, v ), y( u, v ) , z( u, v ) ], ( u, a, b ), ( v, c , d ) ) | var('u,v') ( [ u, u , u^2 + v^2 ] , ( u, -1, 1 ), ( v, -1, 1 ) ) |
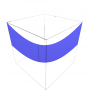 |
| Curvas Parametrizadas | parametric_plot( [ x( t ) , y( t ) , z( t ) ], ( t, a, b ) ) | var( 't' ) parametric_plot3d( [ cos( t ), sin( t ), t ] ,( t , 0, 2*pi ) ) |
 |
| Superfícies definida por Equação | implicit_plot3d( f, ( x, a, b ) , ( y, c, d ) ) | x, y, z = var('x, y, z') implicit_plot3d( x^2 + y^2 + z^2 - 4, ( x, - 2, 2), ( y, - 2, 2 ), ( z,- 2, 2 ) ) |
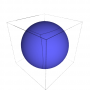 |
Mais sobre o tópico:
Referência: Documentação Sage
Integral
| Operação Matemática | Sintaxe Sage | Exemplo | Resultado |
| $ \displaystyle\int f(x)\rm{d}x$ | integral( f, x ) | integral( x^3, x ) | x^4/4 |
| $\displaystyle\int_{a}^{b}\,f(x)\rm{d}x$ | integral( f , x , a, b ) | integral( sqrt(x) , x, 0 , 4 ) | 16/3 |
| $\displaystyle \int_{a}^{b}\int_{c}^{d}\,f(x,y)\rm{d}x\rm{d}y$ |
var( 'y' ) integral( integral( f, (x, a, b ) ), ( y, c, d) ) |
var( 'y' ) integral( integral( cos(y) , (x, -1, 5 ) ), ( y, pi/6, pi/2) ) |
3 |
| $\displaystyle \int_{a}^{b}\int_{g_1(x)}^{g_2(x)}\,f(x,y)\rm{d}x\rm{d}y$ | integral(integral( f, ( x, a, b) ),(y, g1, g2) ) | integral( integral( x - y, (y, 2*x, 2) ), (x, 0, 1) ) | -1 |
Mais sobre o tópico: ![]() quickref-calc_1.pdf
quickref-calc_1.pdf
Referência: Documentação Sage
Limites
| Operação Matemática | Sintaxe Sage | Exemplo | Resultado |
| $\displaystyle\lim_{x\rightarrow a}f(x)$ | limit(f , x = a ) | limit( x^2+ 2*x, x = 1) | 3 |
| $\displaystyle\lim_{x\rightarrow a^-}f(x)$ | limit( f , x=a, dir =' - ' ) | limit( abs(x)/x, x = 0 , dir=' - ' ) | -1 |
| $\displaystyle\lim_{x\rightarrow a^+}f(x)$ | limit( f , x=a, dir = ' + ' ) | limit( abs(x)/x , x = 0, dir = ' + ' ) | 1 |
| $\displaystyle\lim_{x\rightarrow +\infty}f(x)$ | limit( f , x=+oo ) | limit( 1/x , x = +oo) | 0 |
| $\displaystyle\lim_{x\rightarrow -\infty}f(x)$ | limit( f , x = -oo ) | limit( e^x , x = -oo) | 0 |
Mais sobre o tópico: ![]() quickref-calc_1.pdf
quickref-calc_1.pdf
Referência: Documentação Sage
Matrizes
| Operação Matemática | Sintaxe Sage | Exemplo | Resultado |
| $A= \newcommand{\Bold}[1]{\mathbf{#1}}\left(\begin{array}{rr} a & b \\ c & d \end{array}\right)$ | matrix( [ [ a, b ], [ c, d] ] ) |
A=matrix( [ [ 1, 2 ], [ 1,0 ] ] ) show( A ) |
$\newcommand{\Bold}[1]{\mathbf{#1}}\left(\begin{array}{rr} 1 & 2 \\ 1 & 0 \end{array}\right)$ |
| A + B |
A + B |
A=matrix( [ [ 1, 2 ], [ 1,0 ] ] ) B=matrix( [ [ 0, -1 ], [ 1, 0 ] ] ) show(A + B) |
$\newcommand{\Bold}[1]{\mathbf{#1}}\left(\begin{array}{rr} 1 & 1 \\ 2 & 0 \end{array}\right)$ |
| $\kappa \rm{A}$ | kA | A=matrix( [ [ 1, 2 ], [ 1,0 ] ] ) show(-2*A) |
$\newcommand{\Bold}[1]{\mathbf{#1}}\left(\begin{array}{rr} -2 & -4 \\ -2 & 0 \end{array}\right)$ |
| $\rm{C}^T$ |
transpose( C ) ou C.transpose( ) |
C=matrix( [ [1,2,1], [1,0,1] ] ) show( transpose( C ) ) |
$\newcommand{\Bold}[1]{\mathbf{#1}}\left(\begin{array}{rr} 1 & 1 \\ 2 & 0 \\ 1 & 1 \end{array}\right)$ |
| $\det( \rm{A} )$ |
det ( A ) ou A.det( ) |
A=matrix( [ [ 1, 2 ], [ 1,0 ] ] ) det( A ) |
-2 |
| $\rm{A}^{-1}$ |
A^( -1 ) ou A.inverse() |
A=matrix( [ [ 1, 2 ], [ 1,0 ] ] ) show( A^(-1) ) |
$\newcommand{\Bold}[1]{\mathbf{#1}}\left(\begin{array}{rr} 0 & 1 \\ \frac{1}{2} & -\frac{1}{2} \end{array}\right)$ |
| $\rm{tr}( \rm{A} )$ | A.trace() |
A=matrix( [ [ 1, 2 ], [ 1,0 ] ] ) A.trace() |
1 |
Mais sobre o tópico: ![]() quickref-linalg.pdf
quickref-linalg.pdf
Referência: Documentação Sage
Operações
| Operador | Função Sage | Exemplo | Resultado |
| = | Atribuição | x=1 ; x | 1 |
| + | Adição | 2+7 | 9 |
| - | Substração | 14.5-0.5 | 14 |
| * | Mutiplicação | 3*9+1 | 28 |
| ** ou ^ | Potenciação | 2**5 + 2^2 | 36 |
| / | Divisão | 225/3 | 75 |
| // | Quaciente Inteiro | 10//3 | 3 |
| % | Módulo | 11%2 | 1 |
| > | Comparação( maior que ) | 2>1 | True |
| < | Comparação( menor que ) | 4 < pi | False |
| >= | Comparação( maior ou igual ) | 2 + 3 >= 5 | True |
| <= | Comparação( menor ou igual ) | 11 <= 2*5 | False |
| != ou <> | Comparação( diferente ) | 21 != 3*7 | False |
Mais sobre o tópico:
Referência: Documentação Sage
Vetores
| Operação Matemática | Sintaxe Sage | Exemplo | Resultado |
| $\overrightarrow{v} =(a, b , c)$ | v = vector( [ a, b, c ] ) |
v = vector( [1 , -1, 1 ] ) ; v |
( 1, -1, 1 ) |
| $\overrightarrow{u}+\overrightarrow{v} $ | u + v | v = vector( [ 1, -1, 1 ] ) u=vector( [ 1, 1, 0 ] ) u + v |
( 2, 0 , 1) |
| $k\overrightarrow{v}$ | k*v | v = vector( [ 1, -1, 1 ] ) 2*v |
( 2, -1 , 2 ) |
| $\langle \overrightarrow{u},\overrightarrow{v} \rangle$ | u.dot_product( v ) | v = vector( [ 1, -1, 1 ] ) u=vector( [ 1, 1, 0 ] ) u.dot_product( v ) |
0 |
| $\overrightarrow{u} \times \overrightarrow{v}$ | ( u ).cross_product( v ) | v = vector( [ 1, -1, 1 ] ) u=vector( [ 1, 1, 0 ] ) ( u ).cross_product( v ) |
( 1, -1 , 2 ) |
| $\Vert\overrightarrow{v}\Vert$ | norm(v) | v = vector( [ 1, -1, 1 ] ) norm( v ) |
sqrt(3) |
Mais sobre o tópico: ![]() quickref-linalg.pdf
quickref-linalg.pdf
Referência: Documentação Sage
Para melhor experiência com o SageMath recomendamos fazer uso do SageMathCloud, isso irá permitir você trabalhar com várias planilhas em Sage, IPython, Látex, e muito, muito mais! Experimente!
Caso ainda necessite fazer uso do Software SageMath Desktop você poder fazer downloads em http://www.sagemath.org/download.
O Recursos para para uso de uma célula sage nesta webpage são promovidos por Departamento de Matemáticas, Universidad Autónoma de Madrid.
Seja livre, seja SageMath!


